|
Die
Polarisation [7], [10] gibt die Richtung des Vektors der
elektrischen Feldstärke in der ausgestrahlten
elektromagnetischen Welle an. Man unterscheidet dabei
zwischen linearer und kreisförmiger Polarisation.
Bei der
linearen Polarisation verlaufen die elektrischen
Feldlinien geradlinig. Sind sie senkrecht zur
Erdoberfläche gerichtet, spricht man speziell von
vertikaler Polarisation; verlaufen sie horizontal zur
Erdoberfläche, so liegt horizontale Polarisation vor.
Ist die
Richtung der elektrischen Feldkomponente nicht fixiert,
sondern läuft kontinuierlich in Kreisform, dann spricht
man von zirkularer Polarisation. Je nach Umlaufsinn
unterscheidet man hier noch in rechtsdrehender und
linksdrehender Polarisation.
Die
Richtcharakteristik bzw. Strahlungscharakteristik
beschreibt die Richtungsabhängigkeit der Amplitude,
Phase und Polarisation der von der Antenne erzeugten
Feldstärke. In der Praxis bezieht man sich jedoch nur
auf die Amplitude der elektrischen oder magnetischen
Feldstärke E(j
,J ) bzw. H(j ,J
) oder auf
die von einer Antenne aufgenommene Empfangsspannung U(j ,J
). Es wird
die Richtcharakteristik auf den Maximalwert bezogen
angegeben:
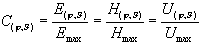 (17) (17)
Betrachtet
man lediglich eine oder mehrere Schnittebenen der
Richtcharakteristik und stellt diese graphisch dar,
erhält man das Richtdiagramm bzw. Strahlungsdiagramm.
Schnitte durch die E-Ebene bzw. durch die H-Ebene werden
speziell Vertikal- und Horizontaldiagramm genannt.
Gegenüber
Rundstrahlantennen, welche in alle Raumrichtungen
annähernd gleich stark strahlen, haben Richtantennen
eine mehr oder minder stark ausgeprägte Vorzugsrichtung.
Der Richtfaktor D
ist das Verhältnis der Strahlungsleistungsdichte Smax
der Antenne in Hauptstrahlungsrichtung verglichen mit der
Strahlungsleistungsdichte des isotropen
Kugelstrahlers als
Referenzantenne bei gleicher Strahlungsleistung Pt [9].
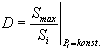 (18) (18)
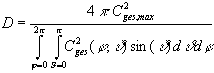 (19) (19)
Der Gewinn G ist das
Verhältnis der Strahlungsleistungsdichte Smax
der Antenne in Hauptstrahlungsrichtung verglichen mit der
Strahlungsleistungsdichte des isotropen
Kugelstrahlers als
Referenzantenne bei gleicher zugeführter
Eingangsleistung Pt0 [7], [9].
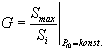 (20) (20)
Der Gewinn
ist über den Antennenwirkungsgrad h mit dem Richtfaktor
verknüpft.
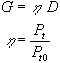 (21) (21)
Wird statt
des isotropen Kugelstrahlers der Hertzsche
Dipol als
Referenzantenne benutzt, gilt:
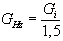 (22) (22)
Bezieht man
sich auf den Halbwellendipol:
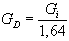 (23) (23)
In der
Praxis wird statt des Gewinnfaktors oft der Gewinnpegel G' = 10 log G in
dB angegeben.

Bild 1
Ersatzschaltbild der Antenne im Sendefall

Bild 2
Ersatzschaltbild der Antenne im Empfangsfall
Der Realteil des Antennenwiderstandes einer
verlustbehafteten Antenne besteht aus dem
Strahlungswiderstand Rr und dem
Verlustwiderstand Rl.
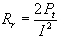 (24) (24)
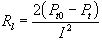 (25) (25)
Der
Strahlungswiderstand des verlustlosen Hertzschen
Dipols beträgt [7]:
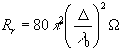 (26) (26)
Für die
Antennenimpedanz eines infinitesimal dünnen
Halbwellendipols mit sinusförmiger Stromverteilung gilt
[6]:
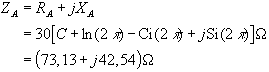 (27) (27)
Dabei ist C
die Eulersche Konstante (C = 0,577215664901532...)
Um nun den
Halbwellendipol bei Resonanz betreiben zu können, muß jXA = 0 werden.
Dieses wird durch kürzen der Dipollänge h um den
Faktor 0,96 erreicht.
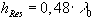 (28) (28)
Antennen
weisen eine bestimmte Induktivität und Kapazität auf,
welche im Gegensatz zu gestreckten elektrischen Leitungen
nicht entlang des Leiters konstant sind. So fällt bei
Antennen die Kapazität zu den Strahlerenden hin ab.
Dieses wird deutlich, wenn man durch Aufklappen einer
Zweidrahtleitung einen Dipol entstehen läßt.
Analog zur
Leitungstheorie wird der Wellenwiderstand einer
verlustlosen Antenne wie folgt definiert [9]:
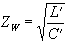 (29) (29)
Dabei ist C' der
Kapazitätsbelag. Er gibt die Kapazität pro
Längeneinheit an der betrachteten Stelle des
Antennenleiters an. Entsprechend ist L' der
Induktivitätsbelag und gibt die Selbstinduktion pro
Längeneinheit an. Werden C'
und L' als
konstant angenommen, so erhält man den mittleren
Wellenwiderstand ZM.
Die in
Gleichung 28 beschriebene elektrische Länge eines
Strahlers gilt nur für einen unendlich dünnen Leiter
der in völlig freier Umgebung betrieben wird. Reale
Dipole müssen schon wegen der mechanischen Festigkeit
eine Mindestdicke besitzen und befinden sich immer in der
Nähe von Bäumen, Häusern und vor allem nahe dem
Erdboden. Dadurch haben die Dipolenden mehr Kapazität
als im Idealzustand, und die Resonanzfrequenz sinkt.
Um die
mechanische Länge einer Antenne zu erhalten, muß der
Verkürzungsfaktor V,
welcher abhängig vom Schlankheitsgrad s der Antenne
ist, berücksichtigt werden.
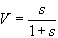 (30) (30)
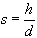 (31) (31)
Es sind h die
Leiterlänge und d
der Leiterdurchmesser der Antenne. Die physikalische
Antennenlänge eines Halbwellendipols erhält man also
aus
 (32) (32)
Ist der
Antenneneingangswiderstand ZA gleich dem
Wellenwiderstand ZL der
Versorgungsleitung, nimmt die Antenne genau den Strom auf,
den die Leitung bei der angelegten Spannung führt. Es
besteht Anpassung. Jede Abweichung bedeutet eine
Fehlanpassung. Dabei kann die Antenne den Strom bzw. die
Spannung nicht vollständig aufzehren, und ein Teil davon
läuft in die Leitung zurück. Ist die Leitung offen oder
kurzgeschlossen, wird die elektromagnetische Welle am
Ende völlig reflektiert, und man spricht von
Totalreflektion.
Ein Maß
für die Anpassung ist der Welligkeitsfaktor s oder das
Stehwellenverhältnis VSWR,
das aus den Amplituden von hin- und rücklaufender Welle
bestimmt wird.
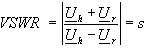 (33) (33)
Die
Bandbreite einer Antenne beschreibt das Frequenzintervall
in dem die elektrischen Eigenschaften dieser Antenne
konstant bleiben bzw. sich nur um zulässige Werte
ändern. Dazu gehören in erster Linie
Man spricht
allgemein von einer Breitbandantenne, wenn innerhalb
einer Oktave das Stehwellenverhältnis
den Faktor 2 nicht überschreitet [14].
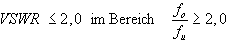 (34) (34)
Als Maß der
Bandbreite wird bei Schmalbandantennen das Verhältnis
von Arbeitsfrequenzintervall zur Mittenfrequenz in
Prozent angegeben:
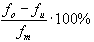 (35) (35)
Bei Antennen
mit größerer Bandbreite als das Verhältnis von oberer
Grenzfrequenz zur unteren Grenzfrequenz:
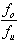 (36) (36)
Die Werte
für fo
und fu
sind abhängig vom Typ und Einsatz der Antenne. Meistens
werden die beiden Eckfrequenzen aufgeführt, in deren
Bereich das Stehwellenverhältnis einen bestimmten Wert
nicht überschreitet.
Bei
Richtantennen ändert sich während entsprechender
Frequenzvariation das Richtdiagramm und die
Hauptstrahlungsrichtung oft mehr als die Eingangsimpedanz.
Hier wird zur Bestimmung der Bandgrenzen die
Formänderung des Richtdiagamms und vereinzelt der Abfall
des Antennengewinns herangezogen.
Oberhalb
einer bestimmten Frequenzgrenze wird die Polarisation von
zirkular polarisierten Antennen zunehmend elliptisch. Zur
Definition der Bandbreite wird hier ein Achsenverhältnis
der Polarisationsellipse von 2:1 als Grenzwert benutzt.
[ <<
Einleitung ] [ Inhalt ]
[ Kapitel 2
>> ]
|
![]() (1)
(1)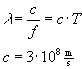 (2)
(2)

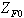 .
.![]() (3)
(3)![]() (Poynting-Vektor)
charakterisiert werden. Er gibt die Richtung und
den Leistungsfluß der Welle je m2 an.
(Poynting-Vektor)
charakterisiert werden. Er gibt die Richtung und
den Leistungsfluß der Welle je m2 an.![]() (4)
(4)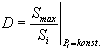 (18)
(18)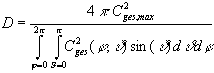 (19)
(19)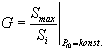 (20)
(20)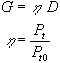 (21)
(21)

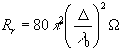 (26)
(26)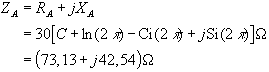 (27)
(27) (32)
(32)